Promising methods for evaluating the winding structure of textile bobbins

Introduction

The relevance of the further development of issues related to forming the cross-wound packages for spinning machines is predetermined by the increased requirements to the quality of packages. This is especially true for packages formed at machines that implement the new spinning techniques – rotor and pneumatic-mechanical, as well as the spinning-torsional and torsional ringless machines.
In this case, the winding’s structure parameters are the following quantities:
– thread’s turn lifting angle β, central angle j between the points of reversal of turns;a distance between thread turns ∆ in the direction perpendicularto the turn;a distance between the turns of thread ∆θ in radialdirection.
Thus, the filament winding is the winding at which the distance between the turns of a thread is smaller than its diameter, dt that is:

Δ ≤ dt                                                             (1)

The tape winding is the winding at which the distance between the turns of a thread is less than three diameters of the thread:

Δ ≤ 3dt                                                           (2)

For commonality of reasoning, we assume that the defective winding structures are formed when:

Δ = kdt                                                           (3)

wherek is the number from 0 to 3, denoting the strictness of requirements to the winding structure. At 0 <k < 1, the winding is the filament one, and at 1<k <3, this is the tape winding. Cylindrical cross-wound packages, produced at spinning machines the type of PPM-120, are used in weaving or knitting industries. Depending on the purpose of yarn, packages are delivered as a weft or a base to textile production after preliminary rewinding or directly from the above-specified machines.The quality of package winding significantly affects thread breakage during the specified operations in textile production.
To determine the reasons for breakages that are categorized in technological practice as breakages due to a violation of the shape of a bobbin and the flyoffs of turns, we additionally monitored the breakage at warping machines. In this case, we controlled a diameter of the winding that experienced a breakage. Control was executed after 8 rollers worked 330 threads each.
To verify this provision, we monitored the breakage at winding machines during winding the bobbins obtained at the spinning-torsional machine PK-100M3. Based on these data, the breakage of thread due to defects in the winding is 58% on average. In this case, the main defect of winding at machine PK-100M3 is the flyoffs of turns that typically accompany braid winding.
The winding structure parameters depend on design of the winding mechanism and affect many technological properties of the package and its capability to processing.
In the case of stationary motion of the system «winding shaft – bobbin» the kinematic ratios between the number of runs of the thread guide and the number of rotations of the bobbin, at which distance Δ=0 are stated in papers [1, 2]. Study [3] reports results of the simulation of the yarn unwinding process from the package and the influence of defects on its quality.
Paper [4], in order to assess the structure of the winding, applies distance Δθ in the circumferential direction between successive turns. It is determined by calculation under conditions of the nonstationary motion of the system «winding shaft – bobbin» only when the gear ratio between the bobbin and the winding shaft is i1. This method certainly cannot be employed to estimate the structure of the winding of the entire package. In many cases, these parameters are determined by the kinematical ratios in the winding mechanism, which is why their analysis employs calculation methods.
A drawback of the described procedure that should be noted is the lack of orientation towards the use of computational equipment, which makes it impossible to check the formation of a braid winding for all diameters.
Paper [5] gives dependence graphs of these magnitudes on order of the braid, that is, on the diameter of the winding, for different thread guide’s motion disturbance laws that apply to disperse winding defects. Using the described procedure, the authors analyzed efficiency of different techniques for dispersing defects in the structure. An analysis of one of the dispersion techniques is given in [6].
To assess the negative effect of the braid winding, it is necessary to obtain a method to analyze the structure of winding in order to determine any possible diameters for braid formation, to define the intensity of this formation, or the thickness they would acquire. In addition, it is desirable that such a method should make it possible to compare the structures of winding, obtained using different winding mechanisms or the same winding mechanism under different modes of its operation.

The aim and objectives of the study

The aim of this study is to develop quality control methods to estimate the structure of cross-wound packages, which would ensure qualitative winding at spinning machines.
To accomplish the aim, the following tasks have been set:
– to clarify the reasons for the formation of defects in the winding structure in the form of the braid and tape winding;
– to investigate experimentally impact of the winding structure defects on suitability of packages for processing during subsequent operations;– to state the generalized criterion for the estimation determination of the winding type.

Procedure for the elaboration of quality control methods to estimate the structure of cross-wound packages.

To solve the set problem, we shall solve inequality |(mL-πDn)sinβ| ≤ kdt  relative to the parameter D:

 

 

 

 

 

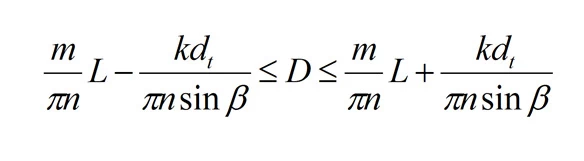
If one requires, when solving (4), an exact match between positions of the successive and preceding turns, that is, k=0, we obtain values for braid diameters:

 

 

 

 

Subtracting from the right side of expression (4) its left side, we obtain a range of diameters over which the inequalities are satisfied:

 

 

 

 

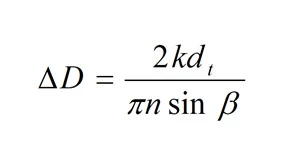
Structure defects arise when the ratio of the layout wavelength L to length of the bobbin’s circumference πD is an irreducible fraction.
At a constant turn lifting angle β this ratio depends only on diameter of the winding D. In the L-πD coordinate system, each ratio L/πD will be matched by a beam passing through the coordinate origin (Figure 1).

 

 

 

 

 

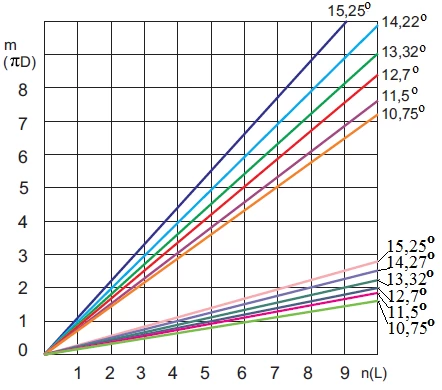
Figure 1. The L-πD diagram.

By analyzing the diagram one can also estimate the strength of the defect. To this end, consider expression (4), from which it follows that the intensity decreases in proportion to the number n. Hence, Fig. 1 shows that the strongest braid m/n=1 under specified conditions forms at the diameter, close to the maximum diameter of the package. Defects that are generated at large values for n are of a smaller thickness. The observations found that the defects generated when n>6 do not affect the quality of the winding, and at n>10 they cannot be detected visually.
Because the L-πD diagram can be built in the dimensionless magnitudes m-n, it can be used to compare the structure of the winding of packages generated at different machines or at the same machine at different settings of the bobbin winder.
Paper [7] shows the relationship between the turns flying off to the end of the package and the winding structure defects. Study [8] pointed to the experimentally established fact of the emergence of flyoffs at the ends, which could be partially eliminated by selecting the angle of turns crossing. This is consistent with the result obtained, however study [8] fails to provide a theoretical explanation of this phenomenon. We estimate a range of diameters ΔD, ever which a defective winding forms, for example, at machine PK-100M3. In this case, we assume n=1 and k=3. The required estimated diameter of the thread can be obtained by employing known formula

 

 

Keywords

Cylindrical, cross-wound

References

F. Jianhui, Y. Jaedeuk, K. Jeong–Suk, J. Yoongho, Journal of Composite Materials 50(16) (2015) 2165-2175.

 

2Patent No. cn 201410607590. “Control System for Textile Winding Machine Convenient for Loading of Bobbin.” ipc: B65H54/547, B65H63/00, B65H67/04. Li L. – No. cn104386539 A, (2015).

 

3S. Praček, N. Pušnik, B. Simončič, F. Tavčer Petra, Fibres and Textiles in Eastern Europe 23(2) (110) (2015) 25-32.

 

4N.S. Ashhepkova, Eastern-European Journal of Enterprise Technologies 7(77) (2015) 54-63.

 

5Patent No. cn 201410607590. “Control System for Textile Winding Machine Convenient for Loading of Bobbin.” IPC: B65H54/547, B65H63/00, B65H67/04. Li L. – No. CN104386539 A, (2015).

 

6M. Nuriyev, I. Seydaliyev, I. Recebov, K. Dadashova, T. Musayeva, Eastern-European Journal of Enterprise Technologies 2(1) (86) (2017) 58-62.

 

7P.N. Rudovsky, News of Higher Educational Institutions, Technology of Textile Industry 6 (1995) 108-111.

 

8F. Maag, Textil industrie 6 (1985) 416-420.

 

9M.N. Nuriyev, T.T. Musayeva, Bulletin of ntu “KhPI” Series: Mechanicaltechnological systems and complexes 49 (1221) (2016) 52-55.

 

10M.N. Nuriyev, F.A. Veliyev, H.I. Həmidov, R.A. Sailov, I.M. Seydaliyev, G.Z. Jabbarova, Ingeniería Solidaria, 14(24) (2018) 17-25.

 

11M.N. Nuriyev, Progressive Technologies and Systems of Mechanical Engineering 4(55) (2016) 44-48.

 

12M.N. Nuriyev, K.S. Dadashova, I.S. Radzhabov, ScienceRise 2(21) (2016) 6-10.

 

13R.A. Jhatial, M. H. Peerzada, U. Syed, Journal of Engineering and Technology 34(1) (2016) 125–32.

DOI: https://doi.org/10.61640/ujeas.2024.1205